Lattice Paths and Generating Functions

02/02 - 2025

Suppose that you are given a piece of graph paper which contains an \(n\) by \(n\) grid. A line is drawn diagonally on the grid from the bottom left point to the top right point. Starting from the origin, you are allowed to move one step at a time - either directly up (north) or directly right (east), but you are never allowed to cross the diagonal line from \((0, 0)\) to \((n, n)\). How many valid paths can you take from the origin to the point \((n, n)\)?

The 14 valid paths for \(n=4\)

I hope that readers of this article who have never encountered this problem will give it a try on their own. If you have already tried, and would like some nudges and hints, I’ve provided some suggestions that I think are helpful (but not too helpful)

• Suppose that someone were to give you a single path from \((0, 0)\) to \((n, n)\) - what ways could you represent that information?
• Are there any properties of the above representation that must be true?
• How many paths are there without the diagonal restriction?
• Does a valid path contain other valid paths?

Introduction

The question which I have just posed is a famous one in combinatorics which counts the number of northeast lattice paths from \((0, 0)\) to \((n, n)\) such that the path never crosses the diagonal. As we will see in due time, the number of valid paths that exists also counts a number of interesting, seemingly unrelated problems.

First, we will explore the most traditional way this problem is solved - graphically and using Dyck words. Then, we will introduce the concept of generating functions, and demonstrate how tools from calculus can be used to solve problems in combinatorics.

The Traditional Approach

If you try taking a swing at this problem then you might find it difficult to answer directly. Indeed, the first time I was tasked with this problem I had a hard time even figuring out where to start with a direct count. When this happens, it can be a useful strategy to start by counting all possible solutions and subtracting the count of solutions which are bad (this technique can also be used to guide missiles…).

As such, let’s begin our journey by answering a much simpler question - how many northeast lattice paths exist from \((0, 0)\) to \((n, n)\) without the restriction that we must not cross the diagonal? This question can be solved rather simply by first imagining what a single path would look like. A solution could be a list of points that we visit (e.g. \((0, 0), (0, 1), (1, 1), \dots\)), but it could also be a list of directions that we would tell someone to take. In other words, a single path \(L\) could be defined as a string consisting of the characters \(N\) and \(E\). So the path that visits \((0, 0), (0, 1), (1, 1), (2, 1), (2, 2)\) would correspond to the string \(NENE\).

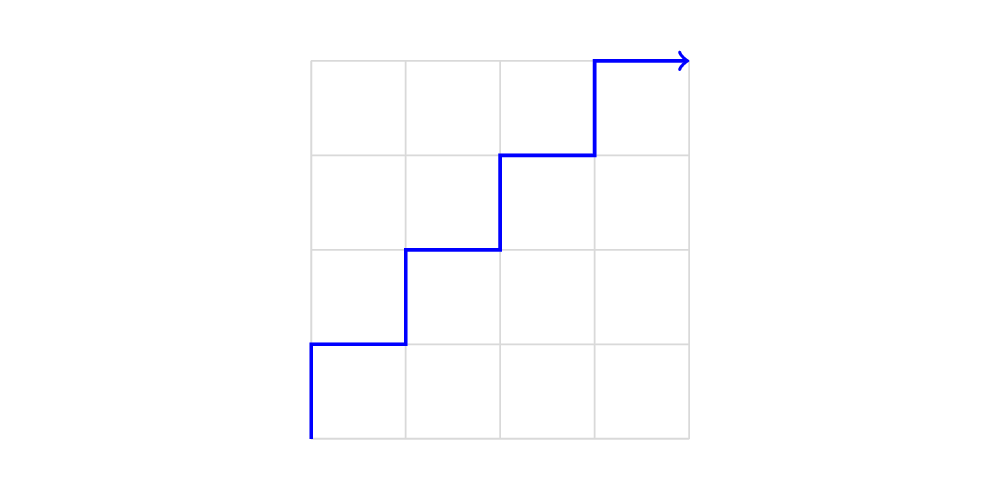The path through \((0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4), (4, 4)\) can be represented by the string \(NENENENE\) as shown above.

With this representation of a path in mind, some properties of a solution become clear. Namely, the string must be exactly \(2n\) characters long, and it must consist of equal parts \(N\) and \(E\). Thus, the number of lattice paths from \((0, 0)\) to \((n, n)\) that may cross the diagonal is clearly given by \({2n\choose n}\) - we have \(2n\) steps to pick, and we have \(n\) locations where we can put the \(N\)s.

To count the number of bad paths, let’s starting by examining a single bad path which we will call \(L\). At some point, by definition, \(L\) cross the diagonal between \((0, 0)\) and \((n, n)\). Imagine we take the path after this point and flip it - what happens to the path now?

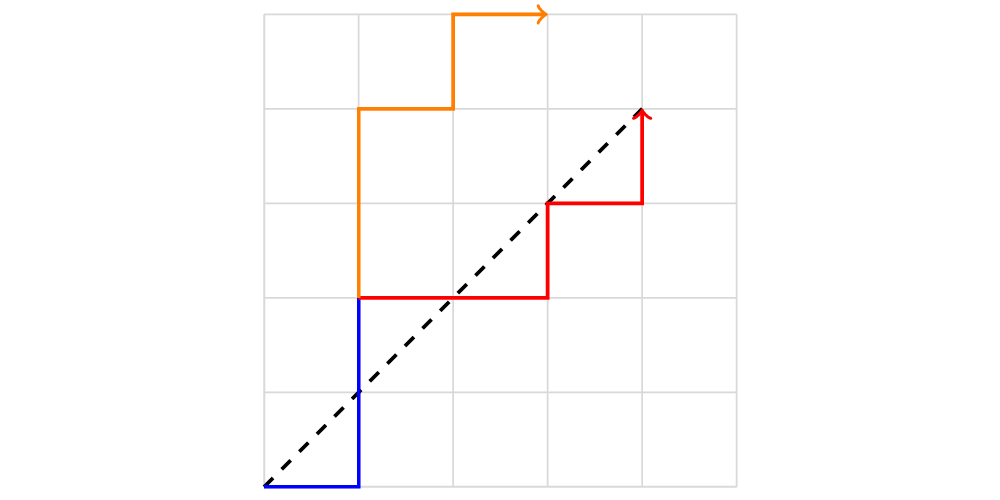Blue and red represent the original path to \((5, 5)\), where blue is the good portion and red is the bad portion. Orange represents the result of “flipping” the bad portion of the path.

By flipping the bad portion of our path, we’ve developed a route which no longer takes us to \((5, 5)\), but rather \((4, 6)\). Why is this of interest to us? Well, we’ve already established that it’s trivial to count any path which goes from the origin to \((i, j)\) without restriction. If it’s the case that all bad paths go to the same point then we can easily count how many bad paths there are.

Identifying whether or not all bad paths go to the same point is going to be difficult to do graphically, however. Let’s lean on our string-based understanding of paths to see if we can generalize the operation that we defined above.

As an example, consider the path above, which is given by \(ENNEENEN\). We can split this into two segments, \(L_1\) and \(L_2\), which represent the blue and red portions, respectively. Then \(L_1 = ENN\) and \(L_2 = EENEN\). The orange path, which we might call \(L_2^\prime\), is given by \(L_2^\prime = NNENE\). We note that \(L_1\) has one more \(N\) than \(E\)’s, since by definition it is the point one step after we cross the diagonal. And we note that \(L_2\) must have one more \(E\) than \(N\), as we established earlier that the whole path must have equal number of \(E\)’s and \(N\)s, and we just established that \(L_1\) has an extra \(N\). And since \(L_2^\prime\) is the inverse of \(L_2\), it must have one more \(N\) than \(E\). So, together, \(L_1\) and \(L_2^\prime\) has two more \(N\)’s than \(E\)’s, meaning it would always go to the point \((n-1, n+1)\).

To formalize this (somewhat), let’s write down a formula that describes the above relationship that is independent of any specific path. Let \(L_1\) be any arbitrary path from \((0, 0)\) to \((i, j)\) where \(j = i + 1\) and \(L_2\) is the path from \((i, j)\) to \((n, n)\). Let \(F_N(x)\) and \(F_E(x)\) be the counts of \(N\)’s and \(E\)’s in the string, respectively. Then \(F_N(L_1) = j\) and \(F_E(L_1) = i\). Likewise, \(F_N(L_2) = n - j\) and \(F_E(L_2) = n-i\). Let \(L_2^\prime\) be the result of flipping \(L_2\). Then \(F_N(L_2^\prime) = n - i\) and \(F_E(L_2^\prime) = n-j\). Then, consider the following quantities:

Likewise,

This is huge! We now have established that all bad paths, once flipped, go from \((0, 0)\) to \((n-1, n+1)\). This means that the number of bad paths can be given by

Note: Astute readers will notice that, in order for this to be a proper proof, we must prove that there is a bijection between bad paths and the inverted path formula that we created. Since this operation is just a trivial swapping of characters, however, I leave that as an exercise for the reader.

Thus, all that remains is to subtract this quantity from our total count to get an answer:

The number above is known in the combinatorics world as \(C_n\), or the \(n\)th Catalan number.

Let’s pause for a moment and briefly consider what other problems are represented by this formula. If we examine the properties of our string-based solution, for instance, we notice that it must also be true that for any character which is selected, it is a valid solution only if the number of \(E\)s proceeding that character equals or exceeds the number of \(N\)s. This is true of another problem which comes up in computer science - balanced parenthesis! This is called a Dyck Word, and it is commonly given to introductory computer science students as a problem to validate whether a given string is a Dyck Word. Here, however, we note that a valid Dyck Word has a bijection to valid northeast lattice paths - simply map \((\to E\) and \()\to N\) and vice versa, and you’ve got yourself a bijection!

Some other problem that are counted by the Catalan numbers include

• The number of full binary trees with \(n+1\) leaves
• For a polygon with \(n+2\) sides, the number of ways that the shape can be divided into \(n\) triangles by connecting vertices is given by \(C_n\).
• The number of permutations of \(\{1,\dots,n\}\) which avoids three-term increasing subsequence (e.g. never contains the string 123)

The Catalan numbers are so ubiquitous in combinatorics that we had a running joke in my first discrete mathematics class that if we didn’t know the answer to a question, it was pretty safe to just guess \(C_n\).

Another Proof Using Generating Functions

Part of what makes the Catalan numbers so interesting is that they can be used to count objects in seemingly unrelated topics - who knew at first glance that the number of full binary trees with \(n+1\) leaves would have the same answer as the number of northeast lattice paths from \((0, 0)\) to \((n, n)\)?

The beauty of the Catalan numbers goes much further than that, however, as there are also numerous, disjoint ways in which they can be derived. The “proof”” above, for instance, is relatively straightforward in that it relies only on the reader being familiar with binomial coefficients (i.e. \(n\) choose \(k\)) to solve. Here, we will present a totally different approach which uses elements from calculus to derive \(C_n\).

An Introduction to Generating Functions

A Refresher on Formal Power Series

One of the most basic building blocks in mathematics is a sequence, which is simply an enumerated, ordered collection of objects. Most people will first encounter sequences during analysis when studying series, which is simply the sum of all elements in a sequence.

A formal power series is a special kind of series in the form

For posterity I will note that a formal power series need not converge, although that is not necessarily relevant to our exploration here. Instead, the key observation I will make is that the power series is uniquely defined by its coefficients, which are simply the elements of the sequence \(a_n\).

Cauchy Products

I’m going to quickly introduce the notion of a Cauchy Product before going any further. While the need for it now is not immediately clear, it will be a useful reference when we try to take products of generating functions later.

Let \(\sum_{i=0}^\infty a_i x^i\) and \(\sum_{j=0}^\infty b_j x^j\) be two power series with complex coefficients. The Cauchy Product of these two power series is given by

Ordinary Generating Functions

Let us introduce generating functions by first creating a sequence of numbers that we wish to count. Suppose that we have a lake with 50 frogs in it. Each month, the number of frogs quadruples from the previous month. On the first day of each month, however, we will also remove 100 frogs and give them to local elementary schools as pets (where they will almost surely meet their demise).

Writing a sequence of numbers that represents this relationship is trivial. We note that \(a_0 = 50\), and that \(a_{n+1} = 4a_n - 100\).

Now, to motivate this, suppose that someone asks how many frogs are in the lake after 100 months. Using the above calculation would require iterating through all 99 prior months in order to get the value of \(a_{99}\) that is required to compute \(a_{100}\). This is immensely wasteful, especially for extremely large values of \(n\). As such, we turn to the previous section and note that a formal power series is defined uniquely by its coefficients. Can we turn our sequence \(a_n\) into a formal power series to simplify this calculation?

To do so, let us start by multiplying both sides of our recurrence relationship for \(a_{n+1}\) by \(x^{n+1}\) and summing over all values of \(n\). In other words

Let us stop briefly to orient ourselves before diving into the weeds. Our goal is to obtain a formula for the generating function \(G(x)\) where \(G(x) = \sum_{n=0}^\infty a_n x^n\) Our formula has \(a_{n+k1}\), however, so we have some work to do to get it there.

First, we note that the left hand side is simply equal to \(G(x) - a_0\), since the only thing missing is the first term. Likewise, we note that the first term on the right hand side is simply \(4x G(x)\). And finally, the value \(\sum_{n=0}^\infty 100 x^{n+1} = \frac{100x}{1-x}\). Thus, we can rewrite this equation as

which leads us to

It may not seem like it, but we’re getting closer to a solution. Recall, again, that a formal power series is uniquely defined by its coefficients. Thus if we can get our equation into the form \(G(x) = \sum_{n=0}^{\infty} y x^{n}\), where \(y\) is some collection of known terms, then \(y\) will give us the coefficient associated with the term \(x^n\).

The first term is easy, and can be rewritten as

The second term is less easy, and requires usage of partial fractions to get into the form we want. I have no interest in explaining partial fractions in my free time, so I will save us all the trouble and simply write down the simplification

Substituting our values in \(G(x)\), we get the following

Thus, computing the number of frogs spared from death in a classroom after month 100 would be as simple as substituting \(n = 100\) into the equation

Writing a Recurrence Relation for the Catalan Numbers

The technique used above to find generating functions required the use of an underlying sequence first. As such, let’s attempt to write down a recurrence relation for the Catalan numbers. We will use our same example of northeast lattice paths above to find one.

Again, suppose that we are to find a northeast lattice path from \((0, 0)\) to \((n, n)\) such that it does not cross the diagonal. When looking for recurrence relations, it can be helpful to imagine a generic solution and see if the solution naturally contains solutions to smaller problems. Indeed, we note that any path from \((0, 0)\) to \((n, n)\) which goes through the point \((i, i)\) for \(0 \lt i \le n\) is a solution for the number of paths from \((0, 0)\) to \((i, i)\).

As such, a tempting way to approach this problem is simply to enumerate all possible splits and take their sums. For instance, \(C_5\) would be counted by \(C_1 C_4 + C_2 C_3 + C_3 C_2 + C_4 C_1\).

To see if this recurrence is correct, let’s spot check our solution by computing some known values. Since we live in a world where \(C_n\) is known, let’s try to compute \(C_5\) given the above relation.

Then

Unfortunately, this number is wrong - \(C_5\) should be equal to 42. Where did we go wrong?

We’ve fallen victim to something called double counting - in short, some of the valid paths that we are counting are counted twice (or more). This is pretty easy to see when you consider that we’ve put no restrictions on how many times a path touches the diagonal before touching \((i, i)\). For instance, the path that goes to \(ENEN\) would be counted both by \(C_1\) and \(C_2\).

How do we remedy this? Well, we can be slightly more deliberate in how we define the splits given above. For our first segment, which we define as the split from \((0, 0)\) to \((i, i)\), we say that the first time it touches the diagonal is at \((i, i)\). This way, the first term in each product is unique.

Doing so restricts the number of paths which are valid, however. Counting the number of paths from \((0, 0)\) to \((i, i)\) where \((i, i)\) is the first time it touches the diagonal is equivalent to counting the number of paths from \((0, 0)\) to \((i-1, i-1)\), since we require that the path beings with an \(N\) and ends with an \(E\).

Thus, our recurrence relation for \(C_5\) would be given by

Which is correct!

Thus, we can write our recurrence relation as:

Establishing the Generating Function for the Catalan Numbers

Let us begin by defining the generic generating function for the Catalan numbers, which we will denote \(C(x)\). Then

where we note that \(C_n\) is the \(n\)th Catalan number.

Next, we can attempt to modify our definition for the generating function in order to get it looking more like our recurrence relation.

And now, using the Cauchy Product that we established earlier

Let’s rearrange this to get something that is too familiar for anyone who has taken highschool algebra

Using the quadratic formula

Note that \(C(x)\) should have just one solution, so we need to determine whether to take the plus or minus from the quadratic equation above. We note that \(C_0 = 1\), so it should be the case that \(\lim_{x\to0} C(x) = 1\) as well.

Taking the case for positive one, we get the following:

For thoroughness we should probably prove that the limit for negative one does exist, but we’ll skip such an exercise for now.

Thus, we’re left with the following form for \(C(x)\)

Note that

Which finally implies that

and thus

And that’s it! Using a recurrence relation and generating functions, we’ve derived the same value for the Catalan numbers as we did using our graphical proof and Dyck words.