josh's site

Properties of Byzantine Fault Tolerant Systems

07/17 - 2025

Imagine that several generals of the Byzantine army have surrounded an enemy city. The generals are stationed rather far apart and communicate by sending runners carrying messages. The army is led by a commanding general, who has put a lieutenant general in charge of each camp. At dusk, the commanding general sends a runner to each lieutenant general ordering a specific course of action (e.g. retreat, attack at midnight, etc). It is now up to the lieutenants to exchange information among themselves to ensure that they will all take the same, and correct, course of action. There is a catch, however - not all the generals are loyal. Some generals, potentially even the commanding general, are traitors and will try their best to stop the loyal generals from reaching consensus on a course of action. Can the loyal generals all agree on the order that was given by the commanding general?

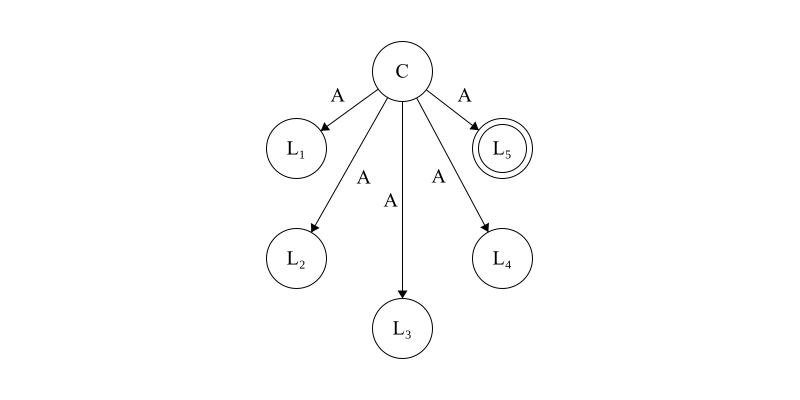
The commanding general, \(C\), sends an order of attack \(A\) to each lieutenant general \(L_1,L_2,\dots,L_5\). \(L_5\), denoted by a double circle, is traitorous.

This scenario, known as the Byzantine Generals Problem, is a foundational problem in distributed computing systems. It deals with achieving consensus between parties in the presence of bad actors who might actively try to thwart attempts at agreement. Generally speaking, a fault refers to some kind of failure in the system (e.g. a general stops sending messages). Inspired by the above scenario, the term Byzantine is used to describe a class of faults where components of a system can exhibit malicious and deceitful behavior.

The seminal paper that introduced this problem, The Byzantine Generals Problem, was authored by Leslie Lamport, Robert Shostak, and Marshall Pease in 1982. A key result from this paper, which is often surprising, is that no solution to the problem exists unless more than two-thirds of the generals are loyal. Or, to put this into concrete numbers, tolerating even a single Byzantine fault requires four generals to be present. More formally, we say that a system with \(n\) nodes is capable of tolerating \(f\) Byzantine faults if \(n \ge 3f + 1\).

Like most problems, the Byzantine generals problem is sensitive to the conditions of its formulation. If we introduce cryptographic signing of messages, for instance, only \(n \ge f + 1\) nodes are needed to tolerate \(f\) faults. If we introduce communication that is asynchronous (i.e. messages do not arrive within a bounded amount of time) then there are no systems which are capable of tolerating even a single Byzantine fault.

This article will be dedicated to understanding how the properties of a consensus problem (e.g. synchronicity, message signing, etc) impacts its feasibility of being Byzantine fault tolerant.

The Byzantine Generals Problem

Let’s start at the beginning of the literature and consider the situation laid out in The Byzantine Generals Problem [1]. At any point in time there are \(n\) generals. We will divide these generals into two groups: a commander and the lieutenants. Please note that the former group has just a single member. The commander will send an order to all \(n - 1\) lieutenants in hope that the following outcomes are met:

  1. All loyal lieutenants obey the same order.
  2. If the commander is loyal, all loyal lieutenants obey that order.

If (1) and (2) are met, we say the system is Byzantine fault tolerant.

We define an algorithm, known as the Oral Message algorithm and abbreviated as \(OM\),which takes on the following definition:

Let’s perform a sample execution where \(f = 1\) and \(n = 4\). We let \(G_1, G_2, G_3\) and \(G_4\) be our generals, and we note that \(G_4\) is the traitor.

The first step of the algorithm, pictured below in Figure 1, has an initial value of \(OM(1)\) with \(G_1\) as the commanding general. \(G_1\) observes a value of \(A\) (which we will note as attack), and sends it to each lieutenant.

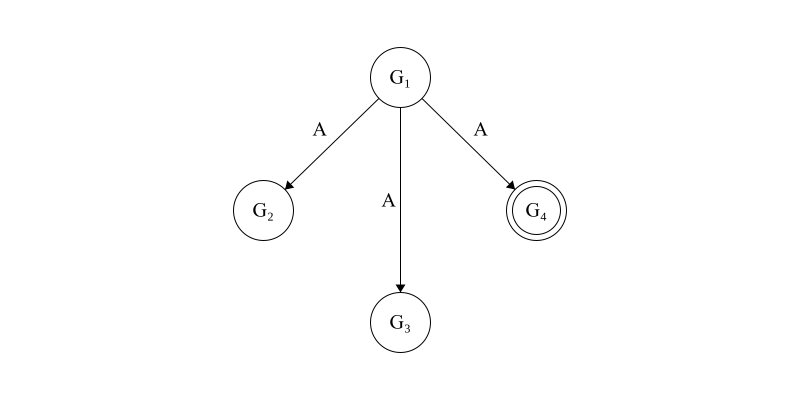
Figure 1. The loyal commanding general, \(G_1\), sends an attack order of \(A\) to all lieutenant generals. \(G_4\), denoted with the double circle, is disloyal.

After this exchange has been completed, each general will observe the following internal state.

\[G_1: v_1 = A,\phantom{aa} G_2: v_2 = A,\phantom{aa} G_3: v_3 = A,\phantom{aa} G_4: v_4 = R\]

Now, each lieutenant will exchange values. First, we let \(G_2\) act as the commanding general and executes \(OM(0)\) with the other lieutenant generals. This is pictured below in Figure 2.

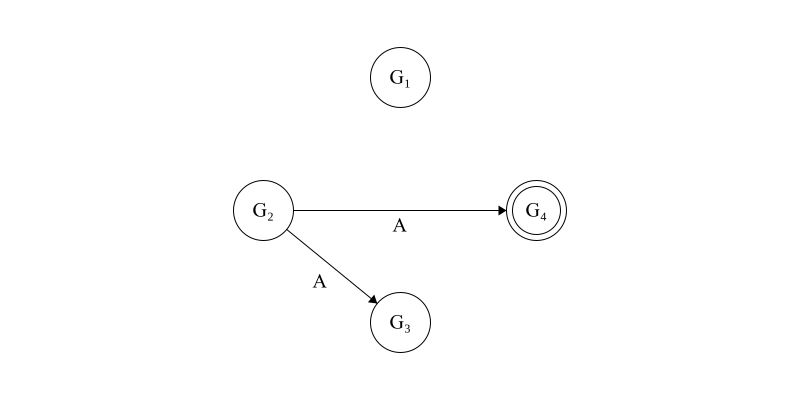
Figure 2. Now \(G_2\), a loyal general, assumes temporary command and shares the value that it learned from the previous step with all other lieutenant generals.

After this exchange, the internal state of each lieutenant will be as follows: \(G_1: v_1 = A\phantom{aa} G_2: v_2 = A\phantom{aa} G_3: v_2 = v_3 = A\phantom{aa} G_4: v_2 = v_4 = R\)

Next, \(G_3\) will assume the commanding role, which is pictured in Figure 3.

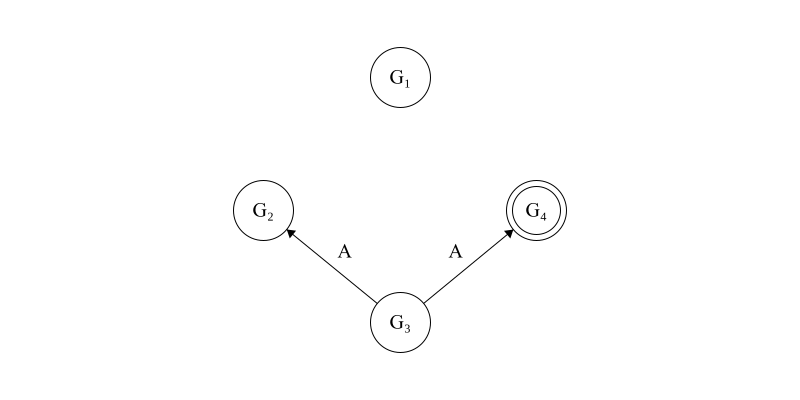
Figure 3. Now \(G_3\), a loyal general, assumes temporary command and shares the value that it learned from the commanding general with all other generals.

After this exchange, the internal state of each general is as follows:

\[G_1: v_1 = A\phantom{aa} G_2: v_2 = v_3 = A\phantom{aa} G_3: v_2 = v_3 = A\phantom{aa} G_4: v_2 = v_3 = v_4 = R\]

Finally, \(G_4\), the disloyal general, assumes command and incorrectly shares it’s internal state with the other lieutenant generals in Figure 4.

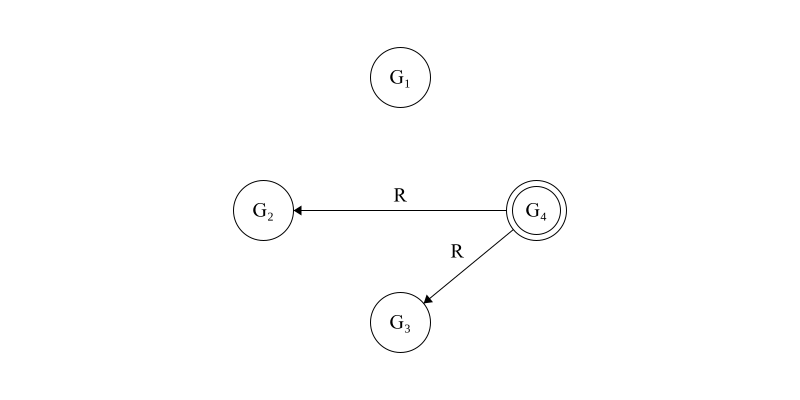
Figure 4. \(G_4\), a disloyal general, lies about it’s internal state with the other lieutenant generals.

After the final round of exchanges, the internal state of each general is as follows:

\[G_1: v_1 = A\phantom{aa} G_2: v_2 = v_3 = A, v_4 = R\phantom{aa} G_3: v_2 = v_3 = A, v_4 = R\phantom{aa} G_4: v_2 = v_3 = v_4 = R\]

In this case, all loyal generals will resolve to an internal value of \(A\) since this is in the majority - meaning that the conditions (1) and (2) stated above are met.

To prove the correctness of this algorithm, we will start by proving the following lemma:

Lemma: For any \(f\) and \(k\), \(OM(f)\) guarantees that if the commanding general is loyal then every lieutenant obeys the order that they sent if there are more than \(2k+f\) generals and \(k\) are disloyal.

Proof. We proceed by induction on \(f\).

The base case is trivial. If \(f = 0\) then there are neither disloyal lieutenants nor commanders. The commander directly sends their commands to the lieutenants, which they obey.

For the inductive case, we assume that \(OM(f - 1)\) satisfies the condition given in the lemma. Our goal is to prove that \(OM(f)\) also satisfies this condition. Let \(i\) represent some arbitrary loyal lieutenant. In \(OM(f)\), we note that (2) involves lieutenant \(i\) applying \(OM(f - 1)\) to all other lieutenants. We note that \(n > 2k + f\), and \(OM(f - 1)\) is applied to \(n - 1\) generals. We also note that \(n - 1 > 2k + (f - 1)\), so we can apply the inductive hypothesis to conclude that lieutenant \(i\) gets the same value \(v\) from all loyal generals. Since there are \(n - 1\) values to compare, we recall that \(n - 1 > 2k + (f - 1) \ge 2k\), and no more than \(k\) generals are traitorous, lieutenant \(i\) will always resolve to \(v\) since \(v\) is in the majority.\(\blacksquare\)

Now we prove that our algorithm works for the Byzantine Generals Problem.

Theorem. For any \(f\), \(n \ge 3f + 1\) implies that \(OM(f)\) satisfies the following conditions 1: All loyal lieutenants obey the same order. 2: If the commanding general is loyal then all loyal lieutenants obey their order.

Proof. We proceed by induction on \(f\).

For the base case we let \(f = 0\). Per the algorithm, the commander, who is loyal, directly sends a command to all lieutenants. Since the lieutenants are all loyal they all follow the commander’s order. Thus, conditions (1) and (2) have been proved directly.

For the inductive case, we assume that \(OM(f - 1)\) satisfies conditions (1) and (2). Our goal is to prove this for \(OM(f)\), and we note that \(f > 0\). We proceed on a proof by cases where the general is either loyal or disloyal.

In the case of a loyal general, we apply the lemma by letting \(k = f\). Since (2) implies (1) then we have proved this for the loyal general case.

In the case of a disloyal general we note that there must be \(f - 1\) disloyal lieutenants. Since \(n \gt 3f\) we note that there are more than \(3f - 1\) lieutenants and since \(3f - 1 > 3(f - 1)\) we can apply the inductive hypothesis to conclude that \(OM(f - 1)\) in step (2) of the algorithm satisfies (1) and (2) in the theorem. Thus, for any arbitrary loyal lieutenant \(i\), they will receive a value of \(v\) from all other loyal lieutenants. Since these other loyal lieutenants are in the majority, (1) is met. \(\blacksquare\)

Impossibility Results

Next, we will demonstrate that the bound of \(n \ge 3f + 1\) is tight - one cannot construct an algorithm which solves the Byzantine Generals Problem with fewer than \(3f + 1\) generals to tolerate \(f\) traitors.

We will forgo a formal proof in this section in favor of a simple example that demonstrates the impossibility of tolerating \(f\) faults with fewer than \(3f + 1\) generals. Let us consider the simple case where \(f = 1\) and \(n = 3\).

In this case, let \(G_1, G_2\) and \(G_3\) be generals who can send orders of either attack (\(A\)) or retreat (\(R\)). We let \(G_1\) be the commanding general.

First, suppose that \(G_3\), a lieutenant, is disloyal. The commander sends a value of \(A\) to both \(G_2\) and \(G_3\). When the lieutenants exchange information, \(G_3\) sends a value of \(R\) to \(G_2\). \(G_2\) has no way to determine which piece of information is truthy and must make a random choice on a course of action. Since this action might be distinct from the commander’s, it clearly does not follow Byzantine fault tolerance. It should be become clear as well that additional rounds of exchange are not helpful in resolving to a proper value - no exchange of information will allow \(G_2\) to determine that \(G_3\) is the one sending it traitorous information.

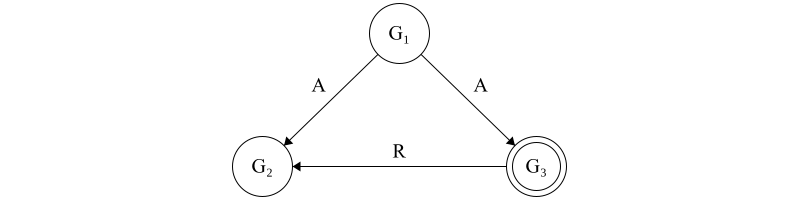
Figure 5. The disloyal lieutenant general, \(G_3\), sends a forged message to \(G_2\). \(G_2\) has no way to differentiate which of the two orders it should follow and so must decide arbitrarily. If this decision does not align with what the loyal commanding general sent, then the loyal generals have disagreed upon their course of action and hence the system is not Byzantine fault tolerant.

The case of a disloyal commanding general is quite similar. In this case, \(G_1\) sends \(A\) to \(G_2\) and \(R\) to \(G_3\). From the point of \(G_2\) this scenario is identical to the previous - it receives a value of \(A\) from \(G_1\) and \(R\) from \(G_3\), with no means to differentiate the two.

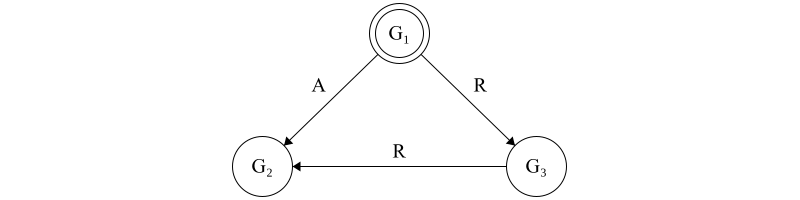
Figure 6. The disloyal commanding general, \(G_1\), sends different messages to the lieutenant generals. \(G_3\) truthfully shares the message it received with \(G_2\). However, \(G_2\) received a different message from \(G_1\) and is again unable to differentiate which one is “correct”.

For an actual proof on the tightness of this bound, I refer readers to Reaching Agreement In the Presence of Faults [2].

Signed Messages

From the impossibility result above, we note that the primary difficulty in tolerating Byzantine faults is that traitorous generals can lie about the messages they have received from other generals. When \(G_3\) sends a message to \(G_2\) about the message it received from \(G_1\) it is allowed to use any value it pleases, and \(G_2\) cannot differentiate this from a real message. What if generals could validate messages they receive?

Adding onto our rather colorful story, we can imagine that each general has a unique signature which is impossible to forge. When a general receives a message they are able to validate with certainty that it came from the general they expected. This does not mean that disloyal generals can no longer act to disrupt the other generals - they still can - the main difference now is that loyal generals are able to detect when messages they receive have been forged. Does this make the problem any easier?

It does! In fact, it makes the problem much easier than it was before. Not only does a three-node solution exist for tolerating a single fault, but in fact \(f\) faults can be tolerated in any system where \(n \ge f+1\).

Let us define a system with signed message as having the following properties:

We propose a new algorithm, denoted as \(SM(f)\), which is tolerant to \(f\) failures so long as \(n > f\).

Let \(V\) be a set of orders and let \(choice\) be a function with the following definition:

\[choice(V) = \begin{cases} v & \text{ if } V = \{v\}\\ \text{ Retreat } & \text{ if } V = \emptyset \end{cases}\]

This definition is taken (almost) directly from [1]. Even non-astute readers might find it interesting that \(choice(V)\) is not defined for cases where \(V\) has more than one element. This is no mistake - it is actually not necessary to prove Byzantine tolerance with any more properties than the above (although the implicit property that \(choice(V)\) is a function and thus always produces the same output for the same input is required). The reason for this will become more clear in the proof.

Let \(x:i\) denote the value \(x\) signed by general \(i\). The string \(v:j:i\) would denote \(v\) signed by \(j\), and then \(v:j\) signed by \(i\). We define \(SM(f)\) as follows:

We define \(V_i\) as the set of orders received by general \(i\) and initialize \(V_i = \emptyset\). The commanding general signs and sends a command to all lieutenant generals. Then, for each \(i\), there are two cases to consider:

  1. If general \(i\) receives a message \(v:0\) and has not received any other order, then
    • We let \(V_i = \{v\}\)
    • General \(i\) sends \(v:0:i\) to all other lieutenants.
  2. If general \(i\) receives a message \(v:0:j_1:\cdots:j_k\) and \(v \not\in V_i\)
    • We add \(v\) to \(V_i\)
    • If \(k \le f\) they send \(v:0:j_1:\cdots:j_k:i\) to every lieutenant other than \(j_1,\dots,j_k\).

When lieutenant \(i\) can receive no more messages, they obey \(choice(V_i)\).

Let us visualize the algorithm for the case where the commanding general, \(G_1\), the disloyal. The complete exchange is described by the following graph.

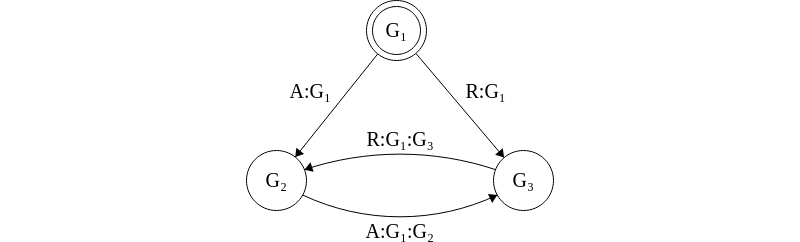
Figure 7. The disloyal commanding general, \(G_1\) sends conflicting orders to the two lieutenant generals.

The key observation to make here is that \(V_{G_2} = V_{G_3} = \{\text{A},\text{R}\}\). Since the two sets are equal then \(choice(V_{G_2}) = choice(V_{G_3})\) and so \(G_2\) and \(G_3\) will obey the same order.

Let us now prove that \(SM(f)\) solves the Byzantine generals problem for \(f\) traitors.

Proof. First, let us consider the case where the commanding general is loyal. Our goal for this case is to prove that all loyal lieutenants obey the general’s order. Since the commanding general is loyal, all lieutenant generals receive \(v:0\) in the first round. For any subsequent round, each general must receive \(v:0\). Receiving a value \(v':0\) would contract the property that modifications to authenticated messages are detectable. Hence, once a loyal general has received all messages, they will execute \(choice(v)\), which we have defined as \(v\). This proves the correctness of the algorithm in the case of a loyal general.

Next, let us consider the case where the commanding general is disloyal. In this case our goal is to demonstrate that every loyal lieutenant general follows the same order. Let \(i\) and \(j\) be arbitrary lieutenant generals - our goal is to prove that if lieutenant \(i\) receives an arbitrary order \(v\) and adds it to \(V_i\) then \(j\) must also receive the same order \(v\) and add it to \(V_j\). Thus, \(V_i = V_j\) and \(choice(V_i) = choice(V_j)\)

The first subcase to consider is that \(i\) received \(v\) directly from the commanding general. In this case, \(i\) sends \(v:0:i\) directly to \(j\), and so \(j\) will insert this value into \(V_j\).

The second subcase is one where \(i\) received \(v\) from some general other than the commander - this would happen if the commanding general sent out conflicting orders. If the value came directly from \(j\) then this case is trivial. If this value did not come directly from \(j\) then we note two more additional subcases. If this is not the last round of exchange then \(i\) directly sends \(v\) to \(j\), and \(j\) will record it. If this is the last round of exchange then we note that there are at most \(f - 1\) disloyal lieutenant generals. This implies there is a single loyal general who must have sent \(j\) the value of \(v\).

This proves that \(SM(f)\) solves the Byzantine generals problem.\(\blacksquare\)

Bibliographic Note

The Byzantine Generals Problem [1] is the seminal paper that popularized the story of loyal and disloyal generals exchanging information in hopes of coordinating an attack. The exact problem which is discussed in this paper is known as Byzantine broadcast - a specific variation of the problem where a single sender (i.e. commanding general) communicates their intent to all other processes. Byzantine broadcast is slightly different than the Byzantine agreement problem where each process starts with their own internal value and exchanges it with all other processes.

The Byzantine Generals Problem [1] makes no mention of the Byzantine agreement variation of the problem - it is strictly concerned with Byzantine broadcast. As such, the bound placed on the \(SM(m)\) algorithm is defined very clearly with the statement “For any \(m\), Algorithm \(SM(m)\) solves the Byzantines generals problem if there are at most \(m\) traitors.”

However, many papers which are concerned with Byzantine agreement will cite [1] and make the claim that \(2f+1\) processes are needed to tolerate \(f\) faults for signed messages. This discrepancy is frustrating as a reader since nowhere in the original paper is \(2f+1\) cited as a bound in any capacity.

As someone outside of academia I can only speculate as to the reason why this discrepancy exists. My intuition is that \(2f+1\) bound is viewed a trivial corollary of the Byzantine agreement and so no papers were published with this bound, hence forcing authors to cite the original paper.

If any reader of this article finds a source which describes this discrepancy, please forward it to me. Until then, I will live in a state of continuous background frustration that academics will state a lower bound with reference to another paper that clearly defines a different lower bound.

The Impossibility of Asynchronous Consensus

So far, we have implicitly assumed the communication between generals is synchronous. Synchronous communication refers to the property that messages are delivered within some known amount of time and, if not, they are considered failures. In the context of the original problem, one might imagine that the commanding general sends their orders at sunrise and expects the generals to decide on a course of action by sundown. There are practical considerations that not all generals will see the sun set at the exact same moment, but the model generally holds for now.

If we modify the formulation of our problem slightly to account for asynchronous communication - messages which are sent and received without any time bound - then the surprising result arises that no algorithm exists which is able to tolerate even a single fault. In fact, this result is strong enough that we can prove the system cannot even handle stopping faults (i.e. a process randomly dying), let alone Byzantine faults. This result, commonly referred to as FLP, was presented by Michael Fischer, Nancy Lynch, and Michael Paterson in their seminal paper Impossibility of Distributed Consensus with One Fault Process [6].

We will begin to prove this result by formalizing the exchange of information between processes. This formalization begins with the introduction of a consensus protocol. A consensus protocol \(P\) has \(n\) processors where \(n \ge 2\). Each process \(p\in P\) has an input register \(i_p\) and an output register \(o_p\) such that \(i_p, o_p\in \{b, 0, 1\}\). A value of \(b\) indicates that the register is in an intermediate (i.e. null) state while the values of zero and one correspond to the choices that the processor can make, which might be analogous to the attack and retreat decisions described in [1]. \(p\) acts deterministically according to some transition function, and we say that once \(o_p\in\{0, 1\}\) it has reached a decision state and cannot change - it is a write once operation. Processes communicate via messages which are defined by a destination \(p\) and a value \(m\).

The function \(\text{send}(p, m)\) enqueues a message \(m\) to be sent to processor \(p\).

The function \(\text{recv}(p)\) attempts to dequeue a message \(m\) for processor \(p\). The function is non-deterministic in the sense that calling \(\text{recv}\) might return \(m\) or it might return \(\emptyset\). Once a message \(m\) has been returned, however, it is deleted from the message queue and will not be returned again.

The state of the system, given by \(S\), is defined by the internal state of each processor and the contents of the message buffer.

A step of the algorithm concerns a single process \(p\). In this step, \(\text{recv}(p)\) is called and the value \(m\) is given to \(p\). \(p\) acts deterministically at this point and may enqueue messages to other processors. Since this step is deterministic, we can can denote \(s\) as a step such that \(s = (p, m)\).

Finally, a schedule \(\sigma\) is a finite or infinite number of steps \(s\) that can be applied to a state \(S\). If the number of steps is finite, let \(\sigma(S)\) be the resulting end state of the system.

We note that the system defined above is commutative. Let \(S\) be a system and let \(\sigma_1\) and \(\sigma_2\) be events. Applying \(\sigma_1\) and \(\sigma_2\) to \(S\) lead to states of \(S_1\) and \(S_2\), respectively. So long as \(\sigma_1\) and \(\sigma_2\) are for different processors, then applying \(\sigma_2\) to \(S_1\) or \(\sigma_1\) to \(S_2\) will lead to the same end state, \(S_3\).

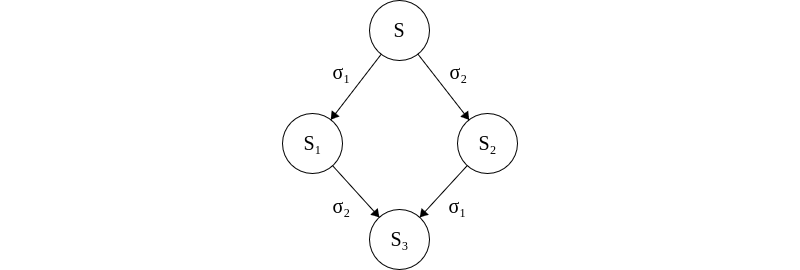
If \(\sigma_1\) and \(\sigma_2\) concern disjoint processes then they can be applied commutatively to \(S\) to reach the same state \(S_3\).

Some state \(S^\prime\) is said to be accessible from \(S\) if a finite set of steps can be applied to \(S\) that result in \(S^\prime\). We say that a state \(S\) is in a decision state \(v\) if there exists a processor \(p\) such that \(o_p = v\). Then a consensus protocol is partially correct if the following conditions are met:

A processor \(p\) is said to be non-faulty if it can take infinitely many steps. If it can take only a finite number of steps, it is said to be faulty. This is a formalization of the stopping fault, where a processor \(p\) suddenly stops handling messages and instead just consumes them without taking any further action or modifying its internal state. A run is admissible if there is at most one faulty process and every message sent to a non-fault process is eventually delivered (i.e. \(\text{recv}(p)\) eventually returns \(m\)). We say that a run is a deciding run if at least on process reaches a decision state. And, finally, we say that a consensus protocol \(P\) is totally correct in spite of one fault if it is partially correct and every admissible run is a deciding run.

With all these definitions out of the way, we can begin to prove the result that no consensus protocol is totally correct in spite of one fault. First, we present a lemma which claims that there must exist an initial state which has a non-deterministic decision.

Lemma 1. Let \(V\) be the set of decision values reachable from \(S\). We say that \(S\) is bivalent if \(|V| = 2\) and univalent if \(|V| = 1\). Then, for some arbitrary consensus protocol \(P\), \(P\) has a bivalent initial state.

Proof. For the sake of contradiction, suppose that there is not a bivalent initial state. This implies that \(P\) is partially correct, so \(P\) must have a 0-valent and 1-valent state by definition. (Note that if \(P\) did not have both 0-valent and 1-valent states then it would imply that the same output is always chosen, which isn’t a particularly interesting consensus problem…). Let us create a chain of initial states such that two states, \(S\) and \(S^\prime\), are adjacent if they differ in the input state of exactly one processor. Since states can be organized in this manner, and there must be 0-valent and 1-valent states by definition, then it follows that there must be adjacent states \(S\) and \(S^\prime\) where one is 0-valent and the other is 1-valent. Now, without loss of generality, let \(S\) be the 0-valent state and \(S^\prime\) be the 1-valent state. Let \(p\) be the processor which has a unique initial state between \(S\) and \(S^\prime\). We have assumed that \(P\) is totally correct in spite of one fault, which means that \(p\) should be able to fail in \(S\) and still decide a value of 0. If we take these exact same sequence of events and apply them to \(S^\prime\) then \(S^\prime\) must now decide 0 instead of 1 (or \(S\) would decide 1 instead of 0). In either case, we arrive at a contradiction since we have demonstrated the existence of a bivalent state.\(\blacksquare\).

The next lemma is the core of the proof, and it is quite dense. The main idea here is that one can delay an event long enough to cause a bivalent state to lead into another bivalent state and enter an infinite loop of undecidedness.

Lemma 2. Let \(S\) be a bivalent state and let \(e = (p, m)\) be some event applicable to \(S\). Let \(\mathbb{S}\) be the set of states reachable from \(S\) without applying \(e\), and let \(\mathbb{D}\) be the set of states that result from applying \(e\) to any state in \(\mathbb{S}\). Then \(\mathbb{D}\) contains a bivalent state.

Proof. For the sake of contradiction, suppose that \(\mathbb{D}\) does not contain a bivalent state.

First, our goal is to prove that \(\mathbb{D}\) contains both 0-valent and 1-valent states. Let \(E_i\) be an \(i\)-valent state reachable from \(S\) for \(i\) in \(0, 1\). We note that \(E_0\) and \(E_1\) must exist because \(S\) is bivalent. For some arbitrary \(E_i\), there are two cases to consider. In the first case, if \(E_i\in\mathbb{S}\), then let \(F_i = e(E_i)\) and clearly \(F_i\in\mathbb{D}\) since it was an element in \(\mathbb{S}\) that had \(e\) applied to it. Then, clearly \(\mathbb{D}\) contains both 0-valent and 1-valent states in this case since we can take \(i\) as 0 or 1. In the second case, \(E_i\) has already had \(e\) applied, which implies that there exists \(F_i\in\mathbb{D}\) such that \(E_i\) is reachable from \(F_i\). Since \(F_i\) is not bivalent, by our claim to contradiction, then \(F_i\) must be \(i\)-valent. Hence, \(\mathbb{D}\) contains both 0-valent and 1-valent states.

Next, consider two states to be neighbors if they differ in exactly one step (this is similar to the argument used in the previous lemma, but with steps rather than processes). Thus, there exists \(S_0, S_1\in\mathbb{S}\) such that \(S_1 = e^\prime (S_0)\) where \(e^\prime = (p^\prime, m^\prime)\). Thus, we consider two cases for the \(p\) in \(e\).

First, if \(p^\prime \ne p\) then this would imply that \(D_1 = e^\prime (D_0)\) from the note early about commutativity. This is a contradiction, however, since the successor of a 0-valent state cannot be a 1-valent state.

All that remains then is the case where \(p^\prime = p\). Since our system is tolerant to one fault, we consider the case in which \(p\) takes no steps. Let \(\sigma\) be the run going from \(S_0\) to a finite deciding run \(A\). By the commutative property of states, \(\sigma\) can also be applied to \(e(S_0)\). Let \(E_i = \sigma(e(C_0))\). Also by the commutative property, \(e(A) = E_0\) and \(e(e^\prime(A)) = E_1\). This would imply that \(A\) is bivalent. This is a contradiction, however, since we defined \(A\) as a finite deciding run.

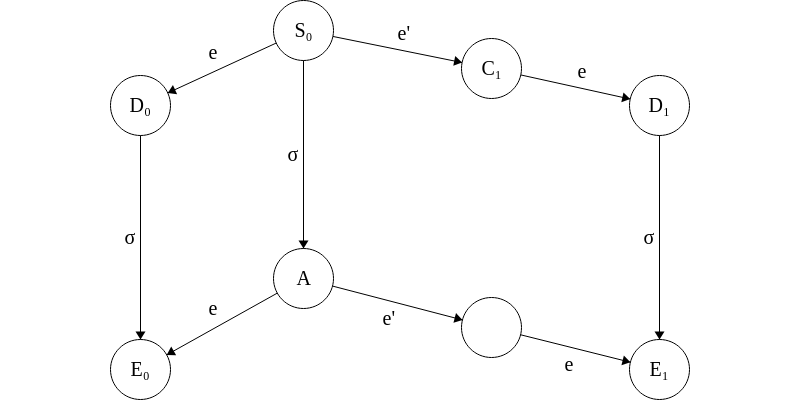
Therefore, we can conclude that \(\mathbb{D}\) contains a bivalent state.\(\blacksquare\)

The previous proof is quite dense and, honestly, difficult to follow without spending a lot of time sitting and thinking about it. The graphic used at the end of the proof should provide a good intuition for the last proof-by-cases, however, which is one of the more difficult parts of the proof.

We now have all the pieces to prove the final theorem.

Theorem. No consensus protocol is totally correct in spite of one fault.

Proof. From Lemma 1, we have proved the existence of a bivalent initial state \(S_0\). Place each processor in a queue and have them receive messages in queue order. When a message is received, put that processor at the back of the queue. Let \(e = (p, m)\cup\emptyset\) be the first message to the first processor in the queue. By Lemma 2, there must exist a bivalent state \(S_1\) reachable from \(S_0\) where \(e\) is the last message received. This argument continues inductively, as we can construct a bivalent state \(S_2\) from \(S_1\) under the same logic. Thus, any arbitrary consensus protocol \(P\) contains an admissible run which never reaches a decision and hence is not totally correct.\(\blacksquare\).

Applications of Byzantine Fault Tolerance

The theory of the Byzantine generals problem emerged from research into safety-critical control systems for aircraft. In the 1970’s, SRI (formerly known as the Stanford Research Institute) was developing a framework called SIFT (Software Implemented Fault Tolerance) which achieved fault tolerance through replicated flight computers. During development, it was found that using three replicas for tasks like clock synchronization was insufficient and prompted the use of additional replicas to compensate [5]. Leslie Lamport and Robert Shostak, who are credited on the original SIFT paper, published Reaching Agreement in the Presence of Faults in 1980 to formalize many of these findings.

Usage of Byzantine fault tolerance in distributed controls systems is the general standard for safety critical applications such as launch vehicles, aircraft, nuclear power plants, and spacecraft. The exact methodology with which systems achieve Byzantine fault tolerance varies across applications, however. Signed messages, which we have seen reduces the lower bound on the number of replicas needed, can be susceptible to false positives given the nature of cryptographic signing (for an interesting discussion I recommend reading Schrödinger’s CRC [4]). As such, many long-duration crewed missions such as Orion (which will hopefully one day take humans back to the moon) use four replicas to achieve Byzantine fault tolerance without signed messages [3]. Shorter duration use-cases, such as launch vehicles missions, can usually circumvent this requirement and get away with just three replicas. Launch vehicles such as SLS and Falcon 9, for instance, both have just three flight computers.

Control systems are an interesting application of Byzantine fault tolerance because they inherently require synchronous communication. By the nature of being real time and running at a fixed cycle rate, it is trivial to define an upper bound on message timeouts to determine that a message has not been received. Thus, avoiding the asynchronous impossibility result is a natural byproduct of a system which runs at a fixed control cycle.

References

[1] Lamport, L., Shostak, R., & Pease, M. (1982). The Byzantine generals problem. ACM Transactions on Programming Languages and Systems, 4(3), 382-401. https://doi.org/10.1145/357172.357176

[2] Pease, M., Shostak, R., & Lamport, L. (1980). Reaching agreement in the presence of faults. Journal of the ACM, 27(2), 228-234. https://doi.org/10.1145/322186.322188

[3] Loveless, A. (2016, November 7). Notional 1FT voting architecture with Time-Triggered Ethernet. NASA Johnson Space Center, Houston, TX. https://ntrs.nasa.gov/api/citations/20170001652/downloads/20170001652.pdf

[4] Pike, L. (2010). Schrödinger’s CRCs. In Proceedings of the IEEE/IFIP International Conference on Dependable Systems and Networks (DSN). IEEE. https://leepike.github.io/pubs/pike-dsn-paper.pdf

[5] Wensley, J. H., Lamport, L., Goldberg, J., Weinstock, C. B., Green, M. W., Levitt, K. N., Melliar-Smith, P. M., & Shostak, R. E. (1978). SIFT: Design and analysis of a fault-tolerant computer for aircraft control. Proceedings of the IEEE, 66(10), 1240-1255. https://doi.org/10.1109/PROC.1978.11114

[6] Fischer, M. J., Lynch, N. A., & Paterson, M. S. (1985). Impossibility of distributed consensus with one faulty process. Journal of the ACM, 32(2), 374-382. https://doi.org/10.1145/3149.214121